直流電源の接続
(RC直列回路)
|
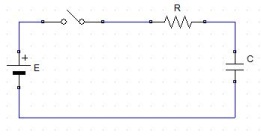
図9.1(a)に示すような回路を考える。この回路でスイッチを閉じると、スイッチが理想的に動作すると考えれば、スイッチオンと同時にそれまで0Vであった抵抗とキャパシタ直列接続部に、Eという電圧が加えられるということである。これを横軸に時間
t をとったグラフで考えると、図9.2のような t<0ではレベル0でt>0ではレベルEとなるステップ状の信号波形で表される(単位ステップ関数u(t)のE倍)。t=0
では理想的には電圧レベルは、0〜E のどこかにあるとされる。
 |
|
 |
|
図9.1(a)
|
|
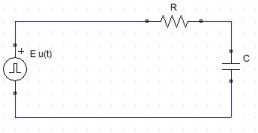
図9.1(b)
|
|
|
|
図9.2
|
図9.1の回路についてキルヒホッフの電圧則により、回路方程式を立てる。

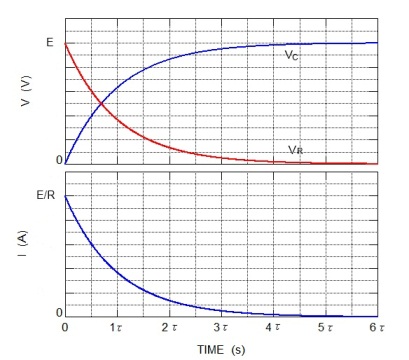
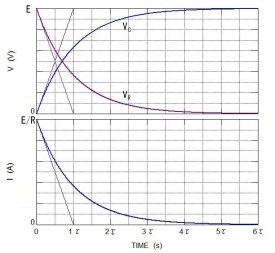
以上の結果の電圧、電流波形を図9.3に示す。ただし横軸のτ=CRとする。
 |
|
図9.3
|
|
直流電源の接続
(RL直列回路) |
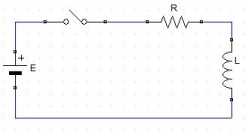
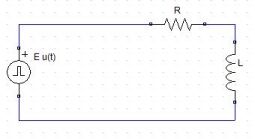
次に、図9.4(a)に示すような回路を考える。図9.1と同様にこの回路でスイッチを閉じると、スイッチが理想的に動作すると考えれば、スイッチオンと同時にそれまで0Vであった抵抗とインダクタ直列接続部に、Eという電圧が加えられるということである。これを横軸に時間
t をとったグラフで考えると、図9.2のような t<0ではレベル0でt>0ではレベルEとなるステップ状の信号波形で表される。t=0
では理想的には電圧レベルは、0〜E のどこかにあるとされる。
 |
|
 |
|
図9.4(a)
|
|
図9.4(b)
|
図9.4の回路についてキルヒホッフの電圧則により、回路方程式を立てる。

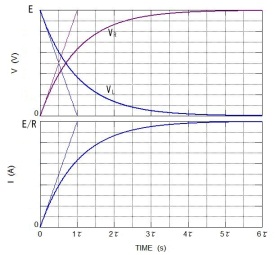
以上の結果の電圧、電流波形を図9.5に示す。ただし横軸のτ=R/Lとする。
 |
|
図9.5
|
|
| 時定数 |
図9.1のRC直列回路や図9.4のRL直列回路は、図9.2のようなステップ波形または方形波が入力されたときに、図9.3や図9.5のように簡単に波形を鈍らせることができる回路である。電気電子回路において、その波形の鈍り具合の目安として、時定数(一般的には「じていすう」と読む。「ときていすう」、「ときじょうすう」とも呼ばれる。)が使われる。時定数の記号としては、τ(タウ)が良く使われる。時定数は、電気電子回路以外の物理学、工学、社会科学においても、システムの応答を示す値として使われている。
RC直列回路において、キャパシタの端子電圧Vcのt=0における曲線の傾きを求めと、
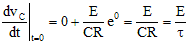
RC直列回路では、τ=CR と定義する。上式で、印加電圧Eが一定なので、τの大きさにより曲線の傾きが決定されることがわかる(図9.6参照。直線が傾きを示す)。
τの単位次元は、C=[クーロン]/[ボルト] と R=[ボルト]/[アンペア]=[ボルト]/([クーロン]/[秒])より
C×R=[秒]となり、時間の次元である。
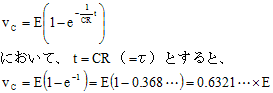
つまり、時定数τの時間が経つと、波形が最終定常値Eの約63.2%(=1-exp(-1))となることがわかる。また、t=2τでは約86.4%、t=3τでは約95.0%、t=7τでは約99.9%となる。
上記と同様にして、RL直列回路において、インダクタ電圧VLのt=0における曲線の傾きを求めると、
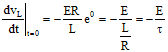
RL直列回路では、τ=L/R と定義される。上式で、印加電圧Eが一定なので、τの大きさにより曲線の傾きが左右されるがわかる(図9.7参照。直線が傾きを示す)。
τの単位次元は、L=[ボルト]×[秒]/[アンペア] と R=[ボルト]/[アンペア]より
L/R=[秒]となり、時間の次元である。
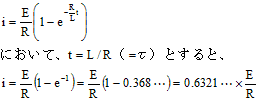
CR直列回路と同様に、時定数τの時間が経つと、波形が最終定常値E/Rの約63.2%(=1-exp(-1))となることがわかる。また、t=2τでは約86.4%、t=3τでは約95.0%、t=7τでは約99.9%となる。
 |
 |
|
図9.6 RC直列回路の電圧電流(直線は接線)
|
図9.7 RL直列回路の電圧電流(直線は接線)
|
|
(クリックで拡大)
|
|
| SPICEによる確認: RC直列回路/RL直列回路の過渡応答をSPICEと数式で解く |
| SPICE回路図ファイル |
Transient_Response_RC.sch Transient_Response_RL.sch (TopSpice 8 回路図ファイル) |
|
|
| 回路図の作成 |
上記でRC直列回路とRL直列回路の回路方程式をそれぞれ解きましたが、その解が合っているかどうかをSPICEで確認します。
回路図の上側は、どちらも信号源として直流電源を接続しています。これは回路図の左側に示したように短い時間(例えば10ns程度)で0Vから立ち上がるパルス信号源を使用しても構いません。
回路図の下側には、微分方程式である回路方程式を解いた結果のキャパシタやインダクタ両端電圧と回路電流を表す数式を、アナログビヘイビア・モデルを使って記述し、それぞれ電圧と電流として発生させています。
|
解析の設定と実行
(過渡解析) |
過渡解析を0〜1msまで行います。ここで注意が必要な点は、信号源がパルス信号源の場合には特別な設定はいりませんが、信号源に直流電源を使用して過渡現象をシミュレーションする場合は、基本的に以下の両方の設定が必要であるということです。(SPICEの種類によってはTopSpiceのように片方だけで良い場合もあります。)
・キャパシタでは初期電圧、インダクタでは初期電流を「IC=」で設定する。(通常はデフォルトでIC=0となっている。)
・過渡解析設定で、UICオプションを有効にする。(過渡解析の初期バイアス計算を行わずIC設定を採用する。)
以上の設定により、直流電源入力がステップ関数として計算処理されることになります。
|
| 解析結果の検討 |
SPICEが過渡解析を行った計算結果の電圧電流波形V(C1)、I(R1)と、微分方程式を解いて求めた結果の電圧電流波形V(C2)、I(R2)が上図のように一致しました。計算が合っていたことが確認できます。なお、SPICEの過渡解析は、数式を解くという解析的にではなく、誤差が一定以下になるまで計算を繰り返し行うという方法で、数値的に解いています。 |
| SPICEによる確認: RC直列回路/RL直列回路の時定数 |
| SPICE回路図ファイル |
Time_Constant_RC2.sch Time_Constant_RL2.sch(TopSpice 8 回路図ファイル) |
|
|
| 回路図の作成 |
RC直列回路の時定数はτ=RCで表されるので、それぞれRとLを単独に2倍3倍にして、時定数の変化を観測します。RL直列回路の時定数はτ=L/Rで表されるので、R固定でLを2倍3倍にした場合、およびL固定でRを1/2、1/3にして時定数の変化を観測します。RC回路、RL回路どちらも変化させたい素子値が2つずつあるので、2つの回路を併記しそれぞれ片方の素子値のみ変化させるようにします。 |
解析の設定と実行
(過渡解析) |
比較のため2つの回路を併記したので、独立に可変させたい値が一つずつあります。通常のパラメトリック解析だけでは、実現できません。このような場合のテクニックとしてTopSpiceのテーブル関数を使っています。適当に変数を設定して(ここではわかり易いようにTAUとしました)、その変数下に実際に可変させたい素子値を表形式で設定できます。パラメトリック解析の設定では、ユーザー変数TAUの値を1,2,3と可変させます。 |
| 解析結果の検討 |
波形が増加しているグラフでは、最終値の63.2%に達するまでの時間が時定数です。減少するグラフでは、初期値の36.8%に達するまでの時間です。素子値を倍増または半減させることにより時定数が2倍となると、電圧電流の波形がどのように鈍(なま)る(または傾く)か確認できます。 |

